Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
The partial tree diagram shows some of the outcomes of flipping a coin four
times. How many possible outcomes are there in all? 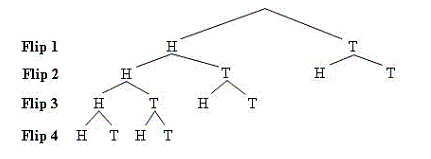
|
|
|
2.
|
You write the numbers 1 through 9 on separate pieces of paper and put them in a
hat. Then you draw the numbers one at a time without replacing them. What is the probability that you
draw the numbers 1 through 9 in order?
|
|
|
3.
|
You have 8 pairs of socks in the dryer. Only one pair is black. You randomly
choose two of the socks. What is the probability that you got both of the black socks?
|
Numeric Response
|
|
|
1.
|
There are 98 lettered tiles in a board game. You randomly draw the tiles shown.
How many of the 98 lettered tiles would you expect to be vowels? 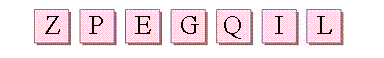
|
|
|
2.
|
A baseball team has won 50% of its games so far. There are 20 regular season
games left. Predict how many of these games the team will win.
|
|
|
3.
|
In a city, there are 10 motorcycles for every 50 people. Predict the number of
motorcycles in a group of 290 people.
|
Short Answer
|
|
|
You have three sticks. Each stick has one red side and one blue side. You
throw the sticks 10 times and record the results. Use the table to find the experimental probability
of the event.
Outcome | Frequency | 3 red | 2 | 3 blue | 0 | 2 blue, 1
red | 5 | 2 red, 1 blue | 3 | | |
|
|
|
1.
|
Tossing 3 blue
|
|
|
2.
|
Not tossing all red
|
|
|
Use the bar graph to find the experimental probability of the event.
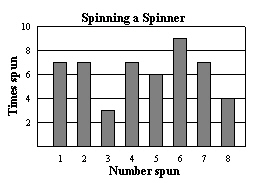
|
|
|
3.
|
Not spinning a 1
|
|
|
Tell whether the events are independent or dependent.
Explain.
|
|
|
4.
|
You flip a coin twice.
First flip: Tails
Second flip: Heads
|
|
|
You randomly choose one of the lettered tiles. Without replacing the first
tile, you choose a second tile. Find the probability of choosing the first tile, then the second
tile.

|
|
|
5.
|
X and U
|
|
|
6.
|
Not X and X
|
|
|
7.
|
You are playing a shell game. A friend shuffles three shells. One of them
contains a pea. You guess which shell contains the pea. If you are wrong, you guess which of the two
remaining shells contains the pea. Is the probability that you find the pea on your first guess
greater than the probability that you do not find the pea in two guesses? Explain.
|